Analiza amortizată evaluează eficiența algoritmilor care prelucrează structuri de date. O listă liniară este o structură de date capabilă să rețină elementele unei mulțimi bine ordonate finite. Coada este o listă liniară în care inserarea se face întotdeauna după elementul adăugat cel mai recent, iar elementul care poate fi șters la un moment dat este cel care a fost inserat cel mai devreme. Principiul de funcționare al acesteia este: First In First Out (primul sosit, primul servit).
În cadrul articolului ne vom concentra asupra unor probleme în care ni se cere să calculăm anumite rezultate referitoare la secvențe maximale ale unui șir care au o anumită proprietate.
În general prin „subșir” înțelegem o parte din elementele unui șir care își păstrează ordinea inițială. Vom numi „secvență” a unui șir orice subșir format doar din elemente aflate pe poziții consecutive.
Observație Un șir cu n elemente are 2n subșiruri, dar doar n(n+1)/2 dintre acestea sunt secvențe (o secvență se termină cu primul element, două se termină cu al doilea, …, n secvențe se termină cu ultimul element al șirului).
O submulțime (deci și o secvență a unui șir) este maximală în raport cu o anumită proprietate dacă are acea proprietate și nu i se mai pot adăuga elemente ale mulțimii în care e inclusă astfel încât să își păstreze respectiva proprietate.
Algoritm general
Forma generală a problemelor prezentate va fi următoarea: se dă un șir x cu n elemente și se cere un rezultat (lungimea maximă, numărul lor etc.) referitor la secvențele acestuia care au o anumită proprietate. Pentru a putea aplica algoritmul este obligatoriu ca proprietatea respectivă să satisfacă următoarea condiție:
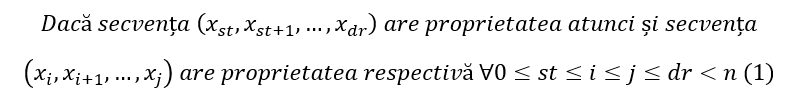
Ceea ce este echivalent cu:

Deși condiția (1) poate părea destul de restrictivă, vom urmări în continuare mai multe exemple de situații în care aceasta e verificată și în concluzie vom putea aplica algoritmul general prezentat în continuare.
Vom folosi o coadă Q în care la fiecare pas i vom păstra cea mai lungă secvență care se termină pe poziția i și are proprietatea cerută. În plus vom demonstra folosind analiza amortizată că algoritmul general propus este unul liniar deși numărul tuturor secvențelor este O(n2).
Algoritmul general este următorul:

Am folosit apeluri ale unor subrutine asociate operațiilor elementare permise în cazul unei cozi Q: PUSH(Q, x) corespunde adăugării lui x în Q, POP(Q) eliminării celui mai vechi element din Q, iar EMPTY(Q) verificării dacă Q este vidă. Trebuie subliniat faptul că fiecare dintre aceste operații se realizează în timp constant (O(1)), nedepinzând de lungimea șirului x sau a cozii Q.
Algoritmul urmărește ca la fiecare pas i coada Q să rețină o secvență maximală cu proprietatea cerută care îl are ca ultim element pe xi. Corectitudinea algoritmului depinde de verificarea proprietății (1′).

Înaintea fiecărui pas i componentele șirului se împart în: elemente care au făcut parte anterior din Q, dar au fost eliminate la pașii anteriori (zona colorată cu roșu), elemente care se află în prezent în coadă (zona verde deschis), xi care urmează să fie adăugat în Q și în fine elementele care urmează să fie prelucrate în etapele următoare (colorate gri).
Elementele din zona roșie nu mai pot face parte din secvența maximală încheiată cu xi conform condiției (1′), prin urmare vor fi ignorate. Elementele secvenței maximale de la pasul anterior vor fi parcurse (eventual în întregime) și trecute în zona roșie atâta timp cât componența cozii nu corespunde unei secvențe valide încheiate pe poziția i. Se obține astfel după un număr de operații care nu depășește lungimea cozii de la pasul anterior cea mai lungă secvență validă încheiată pe poziția i.
Complexitatea algoritmului este O(n) cu O(1) amortizat pentru operațiile din bucla cu test inițial de la linia 9. Putem justifica această afirmație prin fiecare dintre tehnicile prezentate în articolul general referitor la analiza amortizată.
Analiza globală se bazează (ca și în cazul operațiilor efectuate asupra unei stive) pe observația că numărul de iterații ale buclei interioare nu poate depăși numărul de elemente adăugate în coadă, iar acesta este O(n), operațiile de tip PUSH apărând doar la linia 7, care se execută evident de exact n ori.
Același rezultat îl obținem dacă folosim metoda contabilă și asociem costul amortizat 2 pentru operațiile PUSH și respectiv 0 pentru POP.
Definind funcția potențial

obținem de asemenea o sumă a costurilor amortizate care este O(n) și majorează costurile reale, întrucât numărul inserărilor în Q este mai mare sau egal cu cel al eliminărilor. Avem astfel și o justificare a liniarității algoritmului bazată pe tehnica potențialului.
Exemple de utilizare a algoritmului
Am ales pentru exemplificare câteva probleme din categoria „two pointers” aflate pe platforma pbinfo.ro.
Aplicația 1
Problema SecvMaxVal cere pentru un șir de numere naturale și o valoare maximă dată, val, lungimea maximă pe care o poate avea o secvență a șirului cu suma componentelor mai mică sau egală cu val.
O informație esențială este accea că termenii șirului sunt pozitivi. Ținând cont de aceasta rezultă că proprietatea „suma componentelor secvenței este mai mică sau egală cu val” respectă condiția (1) și deci putem aplica algoritmul general prezentat mai sus.
Deși nu este probabil cea mai eficientă variantă de rezolvare, din motive didactice am preferat o implementare în C++ în care am folosit un obiect de tipul queue <int> pentru a reține elementele secvenței maximale cu proprietatea cerută la fiecare pas i.
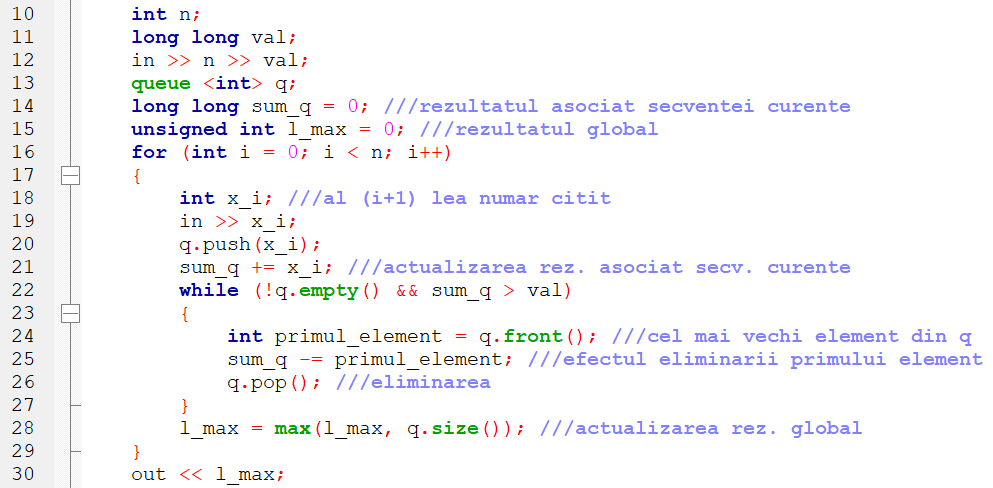
Singurul rezultat global este l_max în care am păstrat lungimea maximă a unei secvențe valide (aceasta coincide evident cu lungimea maximă a unei secvențe maximale valide). Valoarea caracteristică pentru secvența curentă este suma elementelor acesteia, reținută de sum_q. Aceasta crește cu valoarea fiecărui element adăugat în coadă (liniile 20 și 21) și scade odată cu eliminarea unui element (liniile 24, 25 și 26). Condiția ca secvența curentă să fie validă este ca suma elementelor acesteia, sum_q să fie mai mică sau egală cu valoarea cerută val. Prin urmare vom elimina în mod repetat elemente din q, actualizând sum_q cât timp această condiție nu e verificată (liniile 22 – 27).
Aplicația 2
Dacă în cazul problemei anterioare folosirea explicită a cozii putea fi evitată, în cazul următoarei aplicații restricțiile de memorie fac imposibilă o astfel de abordare. Nu putem să reținem toate cele 500000 de numere citite, în schimb observăm că secvențele cerute nu pot avea mai mult de 10000 de elemente (componentele șirului sunt strict mai mari ca 1, deci orice secvență cu produsul egal cu 2k are cel mult k elemente).
Secvența curentă este caracterizată prin produsul elementelor sale. Fiind însă vorba despre puteri ale lui 2, vom reține în coadă exponenții. Mai precis, pentru fiecare xi de forma 2ei vom adăuga în coadă ei. Produsul acestor puteri se reduce de fapt la adunarea exponenților, deci rezultatul caracteristic secvenței curente va fi din nou o sumă. Cum termenii acesteia (exponenții) sunt pozitivi, putem aplica ideea de rezolvare folosită pentru SecvMaxVal, având astfel din nou verificată condiția (1).
Șirul citit poate conține și numere care nu sunt puteri ale lui 2. Observăm că orice secvență care conține un astfel de termen xi al șirului nu este validă. Pentru a ne asigura că astfel de secvențe nu sunt luate în considerare pentru determinarea rezultatului global vom asocia termenilor xi care nu sunt puteri ale lui 2 valori artificiale suficient de mari (strict mai mari decât k).
Implementarea acestei idei este următoarea:

Funcția exponent(x) returnează e în cazul în care x este de forma 2e, respectiv o valoare suficient de mare astfel încât nicio secvență din care face parte x să nu fie considerată validă.

Aplicația 3
A treia problemă a cărei rezolvare o vom prezenta în detaliu este Teatru. Aici este interesantă în special actualizarea rezultatelor caracteristice pentru secvența curentă (și implicit pentru starea cozii). Ne dorim să calculăm cât mai eficient numărul valorilor distincte nr_c_dist. Observația esențială de la care plecăm este că la apariția unui nou costum numărul tipurilor diferite de costume crește doar atunci când avem de-a face cu prima apariție a respectivului tip (condiția de la linia 27) .
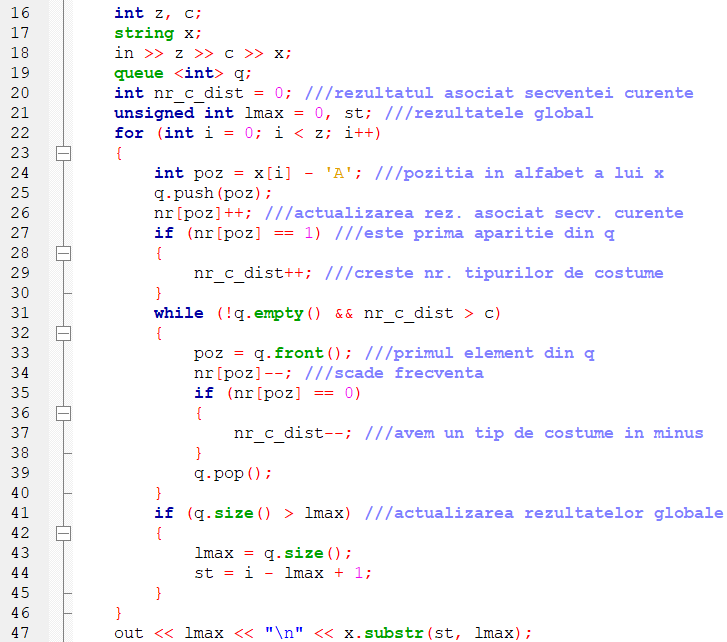
Simetric, numărul tipurilor de costume din secvența curentă (adică numărul valorilor distincte din q) scade doar atunci când frecvența unui tip ajunge la zero (linia 35).
O ultimă observație legată de această problemă e că fiind obligați să afișăm secvența optimă, trebuie să reținem întregul text. În aceste condiții obiectul de tip queue <int> devine practic inutil. O operație de tip PUSH poate fi înlocuită cu mutarea spre dreapta a unui pointer care indică ultimul element al secvenței curente, iar o operație POP cu incrementarea variabilei care reține capătul din stânga al acesteia. De altfel o astfel de tehnică se află la originea termenului „two pointers” – eticheta folosită de pbinfo.ro (și nu numai) pentru acest tip de probleme. Am decis însă, din nou din motive didactice, să păstrăm aceeași abordare pentru a sublinia faptul că raționamentul are la bază o coadă, deși aceasta poate fi implementată în diverse moduri.
Aplicația 4
O problemă clasică interesantă este cea a determinării numărului de triplete care pot fi laturile unui triunghi (suma oricăror două este mai mare ca cel de-al treilea), tiplete formate cu elementele unui șir de numere naturale dat. Problema are o soluție evidentă de complexitate O(n3), dar se pot găsi și rezolvări mai eficiente.
Prima dintre ele (și totodată cea mai cunoscută) se bazează pe căutărea binară: după ordonarea crescătoare a șirului x, pentru fiecare pereche de indici (i, j) cu i<j se caută binar cel mai mare k cu proprietatea că xk<xi+xj, adunându-se la rezultatul global k-j. Cu alte cuvinte, pentru fiecare alegere posibilă a primelor (celor mai mici) două laturi se determină în câte moduri poate fi aleasă cea de-a treia.
Un algoritm chiar mai eficient, de complexitate O(n2) amoritizat este următorul:
- se ordonează crescător șirul;
-
pentru fiecare alegere a celei mai mici laturi xi
- Alegerea celorlalte laturi: pentru fiecare j>i se construiește o coadă în care sunt reținute acele elemente ale lui x care pot reprezenta a doua latură a triunghiului cu latura minimă xi și cea maximă xj;
- suma lungimilor acestor cozi constituie rezultatul cerut.
Ca și în cazul problemelor anterioare, operațiile efectuate la fiecare alegere a celei mai mici laturi reprezintă un nou exemplu de implementare a algoritmului general prezentat anterior, având complexitatea O(n) amortizat.
Condiția (1) este din nou îndeplinită: dacă suma dintre latura minimă și primul element al cozii depășește ultimul element al cozii, atunci și suma dintre latura minimă și o latură mijlocie din coadă depășește o latură mare din coadă. Aceasta se datorează faptului că șirul x a fost anterior sortat.
Un exemplu de implementare a acestei idei poate fi urmărit mai jos:

Adaptarea algoritmului general pentru un context asemănător
Există și probleme în care ni se cere determinarea unui rezultat corespunzător secvențelor minimale cu o anumită proprietate. Dacă proprietatea cerută verifică:
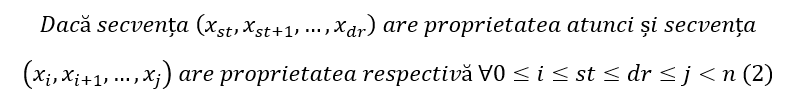
echivalentă cu
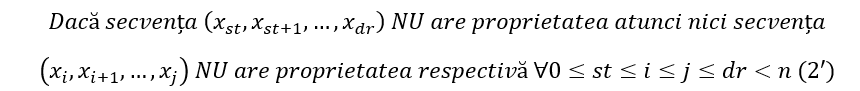
atunci, în mod asemănător putem construi un algoritm general liniar:

Dacă la pasul i găsim o secvență validă terminată cu xi (în urma verificării de la linia 9) căutăm secvența minimală validă încheiată pe poziția i (liniile 11 – 17). Aceasta se obține prin eliminări repetate din coadă cu condiția ca secvența corespunzătoare acesteia să rămână validă.
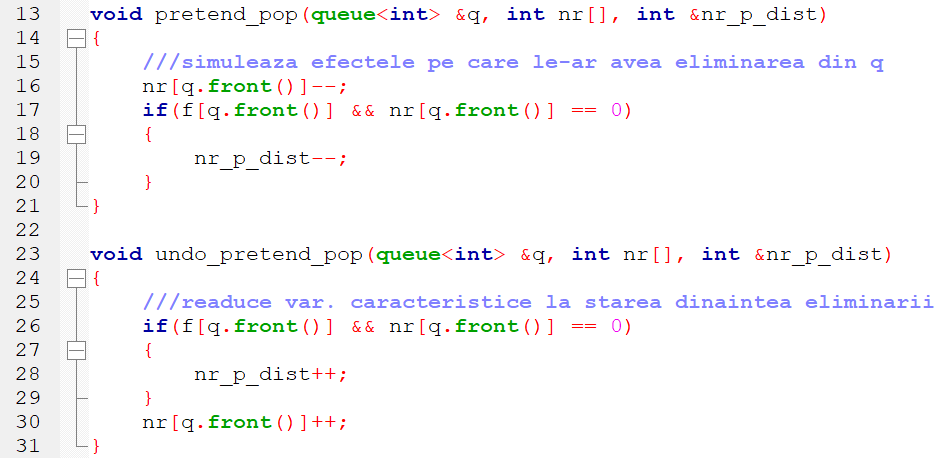
O noutate importantă este apariția operațiilor PRETEND_POP și UNDO_PRETEND_POP. Acestea vor actualiza în timp constant (O(1)) rezultatele caracteristice secvenței curente, reținute de Q. Mai exact PRETEND_POP(Q) calculează valorile caracteristice la care s-ar ajunge în urma unei eventuale eliminări din coadă, iar UNDO_PRETEND_POP(Q) readuce aceste valori la starea dinaintea ultimei eliminări, care de fapt nu a fost operată asupra cozii. Această strategie ne ajută să păstrăm în Q ultima (cea mai scurtă) secvență validă terminată pe poziția i și nu prima (cea mai lungă) secvență care nu verifică proprietatea din enunț.
Aplicația 5
În cazul problemei Panouri proprietatea pe care trebuie să o aibă secvențele este accea de a conține toate elementele unei mulțimi date. Cum valorile elementelor acestei mulțimi sunt relativ mici, vom putea folosi, ca și în cazul problemei „Teatru” un vector de frecvență și o variabilă nr_p_dist care va reține numărul de tipuri de panouri care ne interesează din secvența curentă.
Noutatea este că de data aceasta ni se cere cea mai scurtă secvență cu proprietatea amintită mai sus. Întrucât condițiile (2) și evident (2′) sunt îndeplinite, putem aplica algoritmul general prezentat mai sus. Obținem astfel următoarea implementare în limbajul C++:
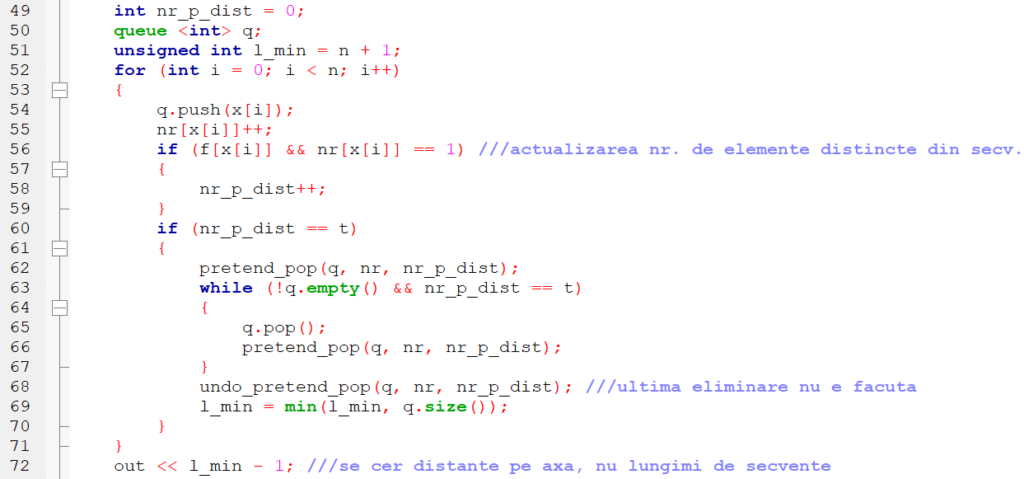
Funcțiile pretend_pop și undo_pretend_pop actualizează rezultatele caracteristice cozii (vectorul de frecvență nr și respectiv numărul de elemente nenule ale acestuiam nr_p_dist).
O ultimă observație se referă la afișarea rezultatului global de la linia 72. În general, distanța dintre panourile de pe pozițiile i și j este j-i, în timp ce lungimea secvenței delimitate depozițiile i și j este j-i+1. Cum din enunț rezultă că avem de-a face cu distanțe pe o axă și nu cu lungimi de secvențe, este necesar să afișăm l_min-1.


