Analiza amortizată este o metodă de evaluare a eficienței algoritmilor care operează asupra unei structuri de date. În cazul în care starea structurii respective se modifică în n etape, analiza amortizată determină complexitatea medie a operațiilor efectuate în cadrul fiecăreia dintre acestea.
Trebuie subliniat faptul că analiza amortizată se aplică pentru cazul cel mai defavorabil al datelor de intrare, calculând o medie a operațiilor efectuate pentru un pas al rezolvării, nu o medie a seturilor de date de intrare posibile. De altfel calculele bazate pe probabilități nu intervin în niciun fel în evaluarea complexității atunci când folosim analiza amortizată.
Există trei metode importante de abordare pentru analiza amortizată: analiza globală (aggregate analysis), metoda contabilă (accounting method) și metoda potențialului.
Vom urmări fiecare dintre cele trei tehnici pentru două probleme clasice: simularea unor operații cu o stivă și incrementarea unui contor binar.
Operații cu stiva:
Algoritmul pe care-l vom analiza este următorul:

unde subrutina MULTIPOP(S, k) este:

Operațiile PUSH(S, x), POP(S) și EMPTY(S) (adăugarea lui x în stivă, eliminarea elementului aflat în vârful lui S și respectiv verifcarea dacă stiva este vidă) au complexitatea O(1). Este evident că în cazul cel mai defavorabil stiva S este plină, având n elemente și deci complexitatea timp a subrutinei MULTIPOP este O(n); cum aceasta e apelată de n ori, la o analiză superficială, am putea deduce că întregul algoritm este pătratic. Vom demonstra însă, folosind fiecare dintre cele trei metode că în realitate avem de-a face cu un algoritm liniar, iar subrutina face în medie un număr constant de operații.
Incrementarea unui contor binar:
Algoritmul general este:

unde subrutina INCREMENT(A) actualizează tabloul binar unidimensional A astfel încât valoarea asociată acestuia
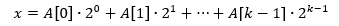
să crească cu 1.

Subrutina INCREMENT(A) are complexitatea O(k), unde k reprezintă numărul de componente ale tabloului și cum aceasta e apelată de n ori, rezultă că întregul algoritm este O(nk). La o privire mai atentă vom constata însă că algoritmul depinde doar de n, având complexitate liniară, iar subrutina execută în medie doar un număr constant de operații
Analiza globală calculează numărul total de operații T(n) ale algoritmului, obținând apoi timpul mediu (amortizat) al fiecăruia dintre cei n pași ca fiind T(n)/n.
În cazul operațiilor efectuate asupra stivei, condiția !EMPTY(S) ne asigură că numărul total de apeluri POP(S), care coincide cu numărul total de iterații ale buclei cât timp nu depășește numărul de apeluri PUSH(S, x) din subrutina principală. Cu alte cuvinte, nu putem scoate din stivă mai multe elemente decât am adăugat.
Dar PUSH este apelată de exact n ori (o dată la fiecare iterație a buclei cu număr cunoscut de pași din subrutina principală). Prin urmare complexitatea timp totală a algoritmului este O(n), ceea ce corespunde unei complexități O(n)/n = O(1) pentru fiecare dintre cei n pași.
Intuitiv, un număr mare de operații executate la un apel al subrutinei MULTIPOP(S, k) înseamnă că stiva S conținea un număr mare de elemente, iar acestea au fost eliminate unul câte unul. Într-o astfel de situație se poate ajunge doar dacă apelurile anterioare ale subrutinei MULTIPOP(S, k) au necesitat puține operații (putem ajunge să avem multe elemente în S doar dacă anterior am eliminat puține). În plus după un număr mare de eliminări S va conține un număr mic de elemente și deci următoarele apeluri ale lui MULTIPOP(S, k) vor necesita de asemenea puține operații.
Analiza incrementării contorului binar se bazează pe calculul numărului de modificări efectuate asupra fiecărui bit (componentă a tabloului A).
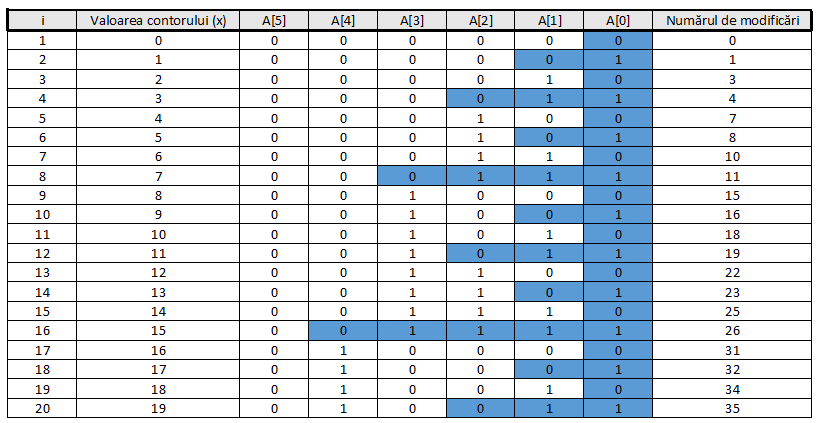
Urmărind cu atenție tabelul de mai sus se observă că A[0] se schimbă la fiecare apel al subrutinei INCREMENT, însă A[1] se modifică numai atunci când A[0]=1, adică doar la jumătate din apeluri, A[2] se modifică la fiecare al patrulea pas ș.a.m.d.. În general
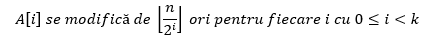
Prin urmare, numărul total de modificări efectuate asupra elementelor tabloului A în urma unei serii de n apeluri de forma INCREMENT(A) este:
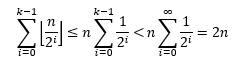
Ca și în cazul operațiilor efectuate asupra stivei complexitatea timp totală este O(n), deci timpul amortizat corespunzător fiecăreia dintre cele n iterații este O(n)/n = O(1).
Metoda contabilă asociază valori diferite pentru operațiile elementare (executate în timp constant) ale algoritmului. Acestea poartă numele de costuri amortizate și, spre deosebire de analiza globală, pot avea valori diferite în funcție de tipul operației. Atunci când costul amortizat depășește costul real, ne putem imagina că am obținut un profit pe care îl vom putea folosi ulterior pentru a acoperi pierderi specifice altor operații.
Dacă notăm cu
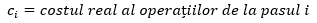
și
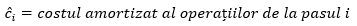
atunci alegerea costurilor amortizate trebuie să urmărească trei obiective: suma costurilor amortizate va trebui să poată fi ușor calculată, să aibă complexitatea dorită (de cele mai multe ori vom arăta că aceasta este O(n)) și aceasta va trebui să depășească (sau să fie cel puțin egală cu) suma costurilor reale, adică:
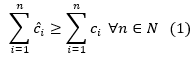
În cazul operațiilor cu stiva vom stabili costul amortizat 2 pentru PUSH(S, x) și costul amortizat 0 pentru POP(S) (în particular subrutina MULTIPOP va avea de asemenea costul amortizat 0). Facem această alegere pe de o parte pentru că numărul operațiilor PUSH este cu siguranță egal cu n (ușor de calculat și evident O(n)), iar pe de altă parte ne bazăm din nou pe observația că din stivă nu pot fi eliminate mai multe elemente decât au fost adăugate și deci:
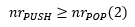
Cum costul real al operațiilor elementare (PUSH și POP) este 1, costul real total este:
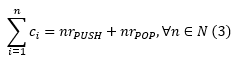
iar costul total amortizat:
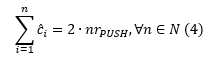
deci ținând cont de (2), (3) și (4) deducem că inegalitatea (1) este verificată.
O interpretare mai accesibilă ar fi următoarea: ne putem imagina activitatea dintr-un restaurant în care sunt strânse farfurii murdare de pe mese (câte una în fiecare unitate de timp) și puse în vârful unui teanc (PUSH(S)). Din când în când un număr de farfurii este luat din vârful stivei și introdus în mașina de spălat vase (MULTIPOP(S, k)). În loc să plătim câte un leu pentru fiecare operație elementară (mutarea unei farfurii de pe masă în vârful teancului sau din vârful stivei în mașina de spălat), care ar corespunde costului real, alegem să plătim câte 2 lei de fiecare dată când o farfurie murdară e luată de pe masă și niciun leu pentru cealaltă operație elementară (costul amortizat). Din suma astfel alocată 1 leu e folosit pentru a plăti mutarea în vârful stivei, iar al doilea rămâne pe farfurie (echivalent unui credit) pentru achitarea transferului ulterior în mașina de spălat. Evident costul real nu poate depăși costul amortizat (de fapt avem egalitate după n pași, doar dacă stiva de farfurii murdare e vidă).
Putem pleca de la un raționament similar și în cazul contorului binar: asociem costul amoritzat 2 (plătim 2 lei) setării unui bit la valoarea 1 și costul amortizat 0 (nu plătim nimic) pentru operația inversă de modificare a valorii unui bit de la 1 la 0. Din nou alegerea costului amortizat ne asigură pe de o parte facilitatea calculului total (subrutina INCREMENT(A) setează cel mult un bit la valoarea 1, deci costul total amortizat e cel mult 2n) și pe de altă parte vom arăta că este ușor să demonstrăm inegalitatea (1).
Costul real este egal cu numărul total de modificări ale biților (0 în 1 și 1 în 0), iar costul amortizat este dublul numărului de transformări de biți din 0 în 1.
Dar orice bit setat la valoarea 0 a fost mai întâi setat la 1, prin urmare numărul de transformări din 0 în 1 (le vom numi trafnsformări 0-1) este mai mare sau egal cu cel al transformărilor inverse (transformări 1-0). De fapt diferența dintre numărul de transformări 0-1 și cel de transformări 1-0 coincide după n incrementări cu numărul de elemente ale tablului A cu valoarea 1.
În concluzie dublul numărului de transformări 0-1 e mai mare sau egal cu numărul total de transformări, deci egalitatea (1) e verificată.
Pentru o mai bună înțelegere putem considera că „plătim” 2 lei pentru fiecare transformare 0-1 și niciun leu pentru transformările 1-0. Din cei 2 lei plătiți pentru o transformare 0-1 un leu e plătit pe loc, iar celălat păstrat sub formă de „credit” pentru o eventuală operație inversă. Numărul de lei achitați în plus față de varianta în care plătim câte un leu pentru fiecare transformare este mereu pozitiv, fiind egal cu numărul de componente care au valoarea 1.
Metoda potențialului urmărește un obiectiv asemănător celui vizat de metoda contabilă: asocierea unui cost amortizat mai mare sau egal cu cel real, mai simplu de calculat și care are complexitatea dorită.
Diferența majoră față de metoda anterioară constă în modul în care se ajunge la acest cost amortizat. Spre deosebire de metoda contabilă, care se concentrează de la bun început asupra costului operațiilor elementare, metoda potențialului vizează structura de date ca un întreg. Mai exact, dacă notăm stările prin care trece aceasta pe parcursul rulării algoritmului cu D0, D1, …, Dn, unde Di reprezintă starea structurii de date după executarea pasului i pentru fiecare i cuprins între 1 și n, iar D0 este starea inițială atunci vom defini o funcție potențial în felul următor:
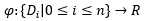
Aceasta asociază câte un număr real fiecărei stări prin care trece structura de date pe parcursul rulării algoritmului. Deși aceasta nu e o regulă, de cele mai multe ori valoarea asociată stării inițiale D0 va fi 0.
Pornind de la funcția potențial vom defini costul amortizat corespunzător fiecărei etape i a algoritmului în felul următor:
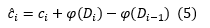
Unde ci reprezintă costul real de la pasul i.
Costul total amortizat al algoritmului pentru n dat devine astfel:
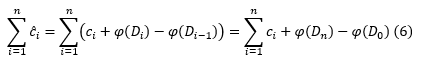
Prin urmare, pentru verificarea inecuației (1) este suficient ca funcția potențial să aibă proprietatea:
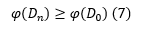
Pentru operațiile efectuate asupra stivei vom defini funcția potențial asociată acesteia ca fiind:
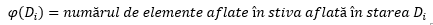
Ținând cont de faptul că stiva este inițial vidă și că nu poate avea un număr negativ de elemente rezultă imediat că inegalitatea (7) și prin urmare și inegalitatea (1) sunt verificate. Rămâne să calculăm costul amortizat total și să arătăm că acesta este O(n).
Vom nota ki = numărul de elemente eliminate efectiv din stivă la pasul i (ki nu coincide neapărat cu valoarea citită pentru k, întrucât e posibil ca stivă să aibă la momentul respectiv mai puțin de k elemente). Atunci costul real al operațiilor de la pasul i va fi:
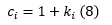
întrucât la pasul i sunt efectuate o inserare în stivă și ki ștergeri, iar potențialul stivei după pasul i devine:
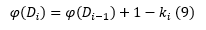
Folosind relațiile (5), (8) și (9) obținem:
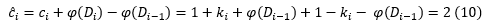
De unde rezultă imediat:
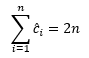
ceea ce, având în vedere că am arătat deja că suma costurilor amortizate majorează suma costurilor reale demonstrează faptul că algoritmul prezentat este într-adevăr liniar. E interesant de remarcat că dacă am calcula costurile amortizate pentru fiecare operație elemntară în parte am obține aceleași valori (2 pentru PUSH și 0 pentru POP și MULTIPOP) ca și în cazul folosirii metodei contabile.
În cazul contorului binar vom defini următoarea funcție potențial:
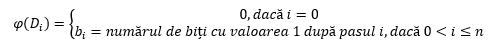
Din definiția funcției rezultă imediat că sunt verificate inegalitățile (7) și (1), deci rămâne să arătăm din nou că avem un cost total amortizat mai mare sau egal cu costul total real.
Urmărind cu atenție funcția INCREMENT observăm că în cadrul acesteia sunt efectuate un număr de transformări de tipul 1-0 pe care-l vom nota cu ti și cel mult o transformare 0-1. Obținem astfel un cost real
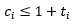
iar
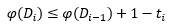
de unde obținem imediat costul amortizat la pasul i:
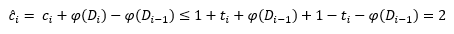
ceea ce conduce la un cost total amortizat mai mic sau egal cu 2n, confirmând din nou liniaritatea algoritmului.
O remarcă interesantă este aceea că algoritmul rămâne liniar chiar dacă valoarea inițială corespunzătoare contorului binar nu este 0. Dacă în starea inițială avem b elemente cu valoarea 1 și notăm din nou cu bi=numărul de biți cu valoarea 1 după pasul i este suficient să modificăm puțin definiția funcției potențial
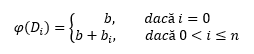
obținând practic aceleași rezultate.


