Sortare topologică

Prof. Boca Alina Gabriela
Colegiul Național de Informatică „Tudor Vianu”, București

Trebuie să vă îmbrăcați pentru a merge să susțineți un interviu important pentru cariera profesională. Care este ordinea în care vă veți îmbrăca?

În imaginea de mai jos sunt prezentate câteva piese de îmbrăcăminte și relația de ordine dintre ele. De exemplu: pentru pantaloni și curea pantalonii trebuie puși înaintea curelei. În imagine este o săgeată care pleacă de la pantaloni către curea care semnifică că pantalonii trebuie puși înaintea curelei:

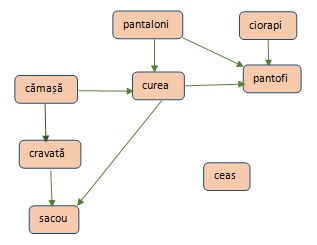
Toate piesele de îmbrăcăminte din imagine pentru care există o relație de ordine sunt reprezentate printr-o relație de ordine, adică printr-o săgeată. În imagine apare și ceasul care poate fi adăugat oricând în procesul de îmbrăcare.

Sortarea topologică realizează o aranjare liniară a pieselor de îmbrăcăminte în funcție de relațiile dintre ele. Orientarea relațiilor corespunde unei ordini în care se poate îmbrăca fiecare dintre piese astfel: se va pune piesa de îmbrăcăminte de la care pleacă săgeata înainte de piesa de îmbrăcăminte unde intră săgeata. De exemplu: se va pune cămașa, apoi cravata și cureaua. Se va pune cravata și cureaua, apoi sacoul.

Sortarea topologică reprezintă plasarea pieselor de îmbrăcăminte de-a lungul unei linii orizontale ca în imaginea de mai jos:

Astfel, dacă avem două piese de îmbrăcăminte a și b, în care piesa a este înaintea piesei b, în înșiruire piesa a trebuie să apară piesa a înaintea piesei b.

Sortarea topologică se poate aplica doar dacă graful orientat (numit și digraf) care se construiește pe baza datelor și a relațiilor dintre acestea este aciclic.

Algoritmul de sortare topologică propus în acest material are la bază gradul intern al fiecărui nod al grafului. Se pornește de la nodurile care au gradul intern zero și se vor adăuga pe parcurs acele noduri, pentru care gradul intern devine zero.

Parcurgerea nodurilor este BFS (Breadth First Search) – este vorba de parcurgerea în lățime, iar nodurile vor fi reținute într-o structură de tip coadă.

La început, se vor adăuga în coadă toate nodurile care au gradul intern 0, adică acele elemente care se vor parcurge la început.

Pentru fiecare nod existent în coadă se vor parcurge toți vecinii lui pentru care există o relație de la nodul curent către vecinii lui. La fiecare parcurgere a vecinilor, se va scădea gradul intern al acestora. Atunci când gradul intern devine 0, acesta se va adăuga la coadă. La finalul cozii se vor adăuga toate nodurile care au gradul intern maxim.

Din algoritmul prezentat în imaginea de mai sus operația sterge muchia u-v se realizează prin scăderea gradului intern al nodului v, iar expresia v nu are muchii înseamnă că gradul intern al lui v este 0.

Algoritmul scris în Limbajul C++ utilizând matricea de adiacență pentru citirea grafului este următorul:

#include <iostream>
using namespace std;
int a[1001][1001],d[1001],c[1001];

int main()
{
    int n,i,j,m,x,y,u,p;
    cin>>n>>m;
    for(i=1;i<=m;i++)
    {
        cin>>x>>y;
        a[x][y]=1; //se creează matricea de adiacență
        d[y]++; //se reține gradul intern al nodului y
    }
    u=1; p=1;
    for(i=1;i<=n;i++)
      if(d[i]==0)
      {c[u]=i; //se adaugă la coadă nodurile care au gradul intern 0
       u++;}
    while(p<=u)
    {
        x=c[p];
        for(i=1;i<=n;i++)
            if(a[x][i]==1)
        {
            d[i]--; //dacă i este vecin al nodului x, se scade gradul său intern
            if(d[i]==0) //dacă gradul intern al nodului i se adăugă la coadă
            {
                c[u]=i;
                u++;
            }
        }
        p++;
     }
     int gasit=0;
     for(i=1;i<=n;i++)
        if(d[i]>0) gasit=1;
     if(gasit==1) cout<<”graful are circuite”;
     else 
        for(i=1;i<=n;i++)
            cout<<c[i]<<" ";
     return 0;
}

Utilizarea matricei de adiacență pentru citirea grafului are câteva limitări. Prima limitare ține de dimensiunea problemei. Nu putem utiliza matricea de adiacență atunci când numărul de noduri depășește valoarea 1000.

O altă limitarea este dată de timpul de execuție. Pentru a căuta vecinii unui nod se parcurge toată linia din matrice, chiar dacă multe dintre elementele aflate pe linie au valoarea 0, chiar dacă nodul respective are un număr mic de vecini.

Soluția la numărul limitat de noduri și la timpul de execuție este dat de utilizarea bibliotecii STL sau a alocării dinamice.

Algoritmul de Sortare Topologică care utilizează biblioteca <vector> din STL este următorul:

#include <fstream>
#include <vector>
using namespace std;
vector <int>v[100002];
int grd_itrn[100002];
int n, m;
int vec_fnl[100002];
int k;

int main()
{
    int a, b;
    cin>>n>>m;
    for(int i=1; i<=m; i++)
    {
        cin>>a>>b;
        v[a].push_back(b);// se creează lista de adiacență a vecinilor nodului a
        grd_itrn[b]++;// se calculează gradul intern al nodului b
    }

    for(int i=1; i<=n; i++)
    {
        if(grd_itrn[i]==0) 
        {
            k++;
            vec_fnl[k]=i; //se adaugă la coadă nodurile care au gradul intern 0
        }
    }

    int p=1, u=k;

    while(p<=u)
    {
        int x=vec_fnl[p];
        for(auto i=v[x].begin(); i<v[x].end(); i++)
        {
            grd_itrn[*i]--; //dacă i este vecin al nodului x, se scade gradul său intern
            if(grd_itrn[*i]==0) //dacă gradul intern al nodului i se adăugă la coadă
            {
                u++;
                vec_fnl[++k]=*i;
            }
        }
        p++;
    }
    int gasit=0;
    for(i=1; i<=n; i++)
        if(d[i]>0) gasit=1;
    if(gasit==1) cout<<"graful are circuite";
    else
        for(int i=1; i<=k; i++)
            cout<<vec_fnl[i]<<" ";

    return 0;
}

Algoritmul de Sortare Topologică care utilizează alocarea dinamică a memoriei:

#include <iostream>
using namespace std;
struct nod
{
    int x;
    nod* urm;
};
nod* v[100001], *prim, *ultim ;
int d[100001];

int main()
{
    int n,i,x,y,m;
    f>>n>>m;
    for(i=1; i<=n; i++)
    {
        v[i]=new nod;
        v[i]->urm =0;
        v[i]->x=i;
    }
    for(i=1; i<=m; i++)
    {
        f>>x>>y;
        d[y]++;// se calculează gradul intern al nodului y
        nod *q, *p;
        q=new nod;
        q->x=y;
        q->urm=0;
        p=v[x];
        while(p->urm)p=p->urm;
        p->urm=q; // se crează lista de adiacență a nodului x
    }
    for(i=1; i<=n; i++)
        if(d[i]==0) // se adăugă la coadă nodurile care au gradul intern 0
            if(prim==0)
            {
                prim=new nod;
                prim->urm=0;
                ultim=prim;
                prim->x=i;
            }
            else
            {
                nod*q=new nod;
                q->x=i;
                q->urm=0;
                ultim->urm=q;
                ultim=q;
            }
    nod *p=prim;
    while(p)
    {
        int a=p->x;
        nod *q=v[a]->urm;
        while(q)
        {
            int y=q->x;
            d[y]--;// scade gradul intern al vecinilor nodului x
            if(d[y]==0) // dacă gradul intern devine 0 se adaugă la coadă
            {
                nod *r=new nod;
                r->x=y;
                r->urm=p->urm;
                p->urm=r;
            }
            q=q->urm;
        }
        p=p->urm;
    }
    int gasit=0;
    for(i=1; i<=n; i++)
        if(d[i]>0) gasit=1;
    if(gasit==1) cout<<"graful are circuite";
    else
    {
        p=prim;
        while(p)
        {
            g<<p->x<<" ";
            p=p->urm;
        }
    }
    return 0;
}

Boca Alina-Gabriela, este profesor de Informatică la Colegiul Național de Informatică Tudor Vianu, din București. A absolvit secția Informatică din cadrul Facultății de Matematică, Universitatea din Bucuresti, are un master în Baze de Date și servicii Web și un master în Științele Educației. Este pasionată de tot ce este inovator în domeniul IT și în educație.