Turnurile din Hanoi – recursivitate, Divide et Impera (animat)

Despre metoda “Divide et Impera”

Divide et Impera este o tehnică specială şi se bazează pe un principiu extrem de simplu: descompunem problema în două sau mai multe subprobleme (mai uşoare), care se rezolvă, iar soluţia pentru problema iniţială se obţine combinând soluţiile problemelor în care a fost descompusă. Se presupune că fiecare dintre problemele în care a fost descompusă problema iniţială, se poate descompune în alte subprobleme, la fel cum a fost descompusă cea iniţială. Procedeul se reia până când (în urma descompunerilor repetate) se ajunge la probleme care admit rezolvare imediată.

Evident, nu toate problemele pot fi rezolvate prin utilizarea acestei tehnici. Fără teama de a greşi, putem afirma că numărul lor este relativ mic, tocmai datorită cerinţei ca problema să admită o descompunere repetată.

Divide et Impera este o tehnică ce admite o implementare recursivă. Am învăţat principiul general prin care se elaborează algoritmii recursivi: ce se întâmplă la un nivel, se întâmplă la orice nivel (având grijă să asigurăm condiţiile de terminare). Tot aşa, se elaborează un algoritm prin Divide et Impera. La un anumit nivel, avem două posibilităţi:
1) am ajuns la o problemă care admite o rezolvare imediată, caz în care se rezolvă şi se revine din apel (condiţia de terminare);
2) nu am ajuns în situaţia de la punctul 1, caz în care descompunem problema în două sau mai multe subprobleme, pentru fiecare din ele reapelăm funcţia, combinăm rezultatele şi revenim din apel.

Turnurile din Hanoi

Cerință. Se dau 3 tije simbolizate prin a, b, c. Pe tija a se găsesc discuri de diametre diferite, aşezate în ordine descrescătoare a diametrelor privite de jos în sus. Se cere să se mute discurile de pe tija a pe tija b, utilizând ca tijă intermediară tija c, respectând următoarele reguli:
• la fiecare pas se mută un singur disc;
• nu este permis să se aşeze un disc cu diametrul mai mare peste un disc cu diametrul mai mic.

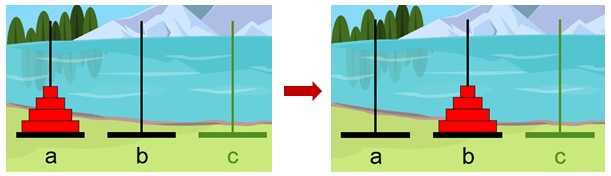
Rezolvare. Să începem ușor. Dacă n=1, se face mutarea “ab“, adică se mută discul de pe tija a pe tija b.
Dacă n=2, se fac mutările “ac“, “ab“, “cb“. În cazul în care n>2, problema se complică.

Notăm cu H(n,a,b,c) şirul mutărilor celor n discuri de pe tija a pe tija b utilizând, ca tijă intermediară, tija c.

Conform strategiei Divide et Impera, încercăm să descompunem problema în alte două subprobleme de acelaşi tip, urmând apoi combinarea soluţiilor. În acest sens, observăm că mutarea celor n discuri de pe tija a pe tija b, utilizând ca tijă intermediară tija c, este echivalentă cu:

• mutarea a n-1 discuri de pe tija a pe tija c, utilizând ca tijă intermediară tija b;
• mutarea discului rămas pe tija b;
• mutarea a n-1 discuri de pe tija c pe tija b, utilizând ca tijă intermediară tija a.

Parcurgerea celor trei etape permite definirea recursivă a şirului H(n,a,b,c) astfel:

Astfel, pentru n=2 avem:

H(2,a,b,c) = H(1,a,c,b),ab,H(1,c,b,a) = ac,ab,cb

iar pentru n=3 rezultă:

H(3,a,b,c) = H(2,a,c,b),ab,H(2,c,b,a) = H(1,a,b,c),ac,H(1,b,c,a),ab,H(1,c,a,b),cb,H(1,a,b,c)
= ab,ac,bc,ab,ca,cb,ab.

Algoritmul redactat în limbajul Logo este prezentat mai jos:

var "a "a
var "b "b
var "c "c
procedura hanoi :n :a :b :c
    daca (:n <= 0)
    [ afiseaza "Nimic! ]
    daca_altfel (:n = 1)
    [ afiseaza (cuvinte :a :b) ]
    [
        hanoi :n-1 :a :c :b
        afiseaza (cuvinte :a :b)
        hanoi :n-1 :c :b :a
    ]
sfarsit
hanoi 3 :a :b :c 

Varianta animată o găsiți în cadrul platformei:
[acces la programul animat]

Observații. Pentru varianta interactivă am folosit cele două variabile globale ":lgv1" (numărul de discuri) și ":lgv2" (timpul de tranziție în milisecunde). Puteți alege numărul de discuri între 1 și 9 (în funcție de complexitate, recomand un timp cât mai mic de executare - de exemplu pentru 9 discuri, aș alege 10ms).

În loc să fie afișate pur și simplu mutările, am creat un subprogram numit "hanoi_grafic" care face apel la altele, precum "tija" care la fiecare iterație reinițializează ecranul, ori "tije" care trasează discurile corespunzător. Nu voi detalia programul, însă vă invit să îl analizați!

Problema "Turnurilor din Hanoi" - scurt istoric & sfârșitul Universului

Turnurile din Hanoi au foarte puțin de-a face cu cele din Vietnamul zilelor noastre. François Édouard Anatole Lucas (cunoscut ca Édouard Lucas) a fost un matematician francez care a trăit între anii 1842-1891. În studiul său, "Récréations Mathématiques, Vol. 3, pp. 55–59, Gauthier-Villars, Paris, 1893", a notat faptul că există în templul Kashi Vishwanath, Varanasi, India, un set de 64 de discuri de aur (foarte fragile) pe 3 tije diamantate numite "Turnurile din Brahma".

Călugării încearcă să rezolve problema matematică "de la începuturile timpului". Deși aparent o poveste imaginară, o legendă, problema necesită 2⁶⁴−1 = 1.84 × 10¹⁹ mutări pentru a fi rezolvată. La o mutare pe secundă sunt necesare 5.85 x 10¹¹ ani. Problema are deci complexitate exponențială.

Așadar, poate 42 este numărul ce definește Viața, Universul și Totul, iar Universul se va termina atunci când acei călugări vor rezolva problema matematică. 🙂 Interesant, nu?

S.T.E.M. și mai mult - experiment didactic acasă

Consider că principiul S.T.E.M. transcende știința, tehnologia, ingineria și matematica - cele patru guvernează tot ceea ce este în jurul nostru. Oriunde privești este știință, matematică, logică. Uneltele noastre sunt multiple, poți să plătești pentru copilul tău un joc scump ori să îl creezi în timp ce pregătești cina:

Succes și distracție plăcută!